Humanidades
O sistema de IA TongGeometry gera e resolve problemas de geometria de nível olímpico
O novo sistema de IA, TongGeometry, tem um desempenho tão bom quanto o de olimpíadas humanas de elite em um domínio que exige profunda criatividade e raciocínio.
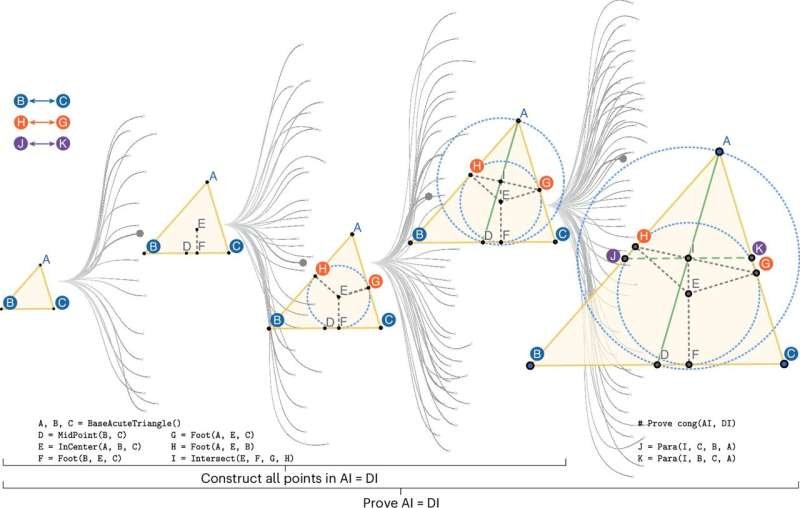
Busca em árvore guiada por TongGeometry para geração e solução de problemas de geometria simétrica. Crédito: Nature Machine Intelligence (2026). DOI: 10.1038/s42256-025-01164-x
A Olimpíada Internacional de Matemática (IMO) é uma competição prestigiosa que reúne estudantes talentosos do ensino médio de todo o mundo, nos quais os competidores resolvem problemas matemáticos complexos. Os problemas de geometria presentes nesse tipo de competição — em particular, a lógica formal e o raciocínio espacial envolvidos — têm sido considerados um parâmetro fundamental na pesquisa em inteligência artificial (IA).
Agora, uma equipe na China desenvolveu um sistema de IA capaz tanto de resolver quanto de gerar problemas de geometria de nível olímpico. O novo sistema de IA, TongGeometry, tem um desempenho tão bom quanto o de olimpíadas humanas de elite em um domínio que exige profunda criatividade e raciocínio. Suas conquistas são detalhadas no novo estudo da equipe de pesquisa, publicado na Nature Machine Intelligence .
Raciocínio automatizado em geometria
Alguns sistemas de IA são atualmente capazes de resolver problemas de geometria de nível olímpico, mas propô-los exige domínio matemático, bem como sensibilidade estética, o que é difícil de alcançar em sistemas de IA. Sistemas anteriores, como o AlphaGeometry, focavam apenas na resolução de problemas e ainda assim exigiam recursos computacionais significativos.
Os autores do estudo escrevem: "Os problemas mais admirados exibem uma simplicidade enganosa: acessíveis por meio de conhecimento fundamental, mas exigindo profunda criatividade para soluções completas. A elegância matemática, particularmente a simetria em suas diversas formas, serve como um critério de qualidade essencial em competições de prestígio."
A natureza visual e construtiva da geometria apresenta obstáculos para a IA. Limitações fundamentais surgem nas abordagens computacionais para problemas de geometria em olimpíadas devido à "explosão combinatória de caminhos de raciocínio e à escassez de problemas exemplares para o desenvolvimento de heurísticas", segundo os autores do estudo.
Arquitetura neural do tipo ator-crítico de TongGeometry para resolução de problemas geométricos. Crédito: Nature Machine Intelligence (2026). DOI: 10.1038/s42256-025-01164-x
TongGeometry: Proponente e solucionador de problemas de nível olímpico
O TongGeometry, um sistema neurosimbólico que utiliza uma busca guiada em árvore com uma estrutura Markoviana para modelar o raciocínio geométrico, parece superar em grande parte os obstáculos apresentados por esses problemas de geometria. A equipe desenvolveu o sistema ajustando dois grandes modelos de linguagem — um que sugere direções de busca e outro que estima as etapas de raciocínio.
Utilizando 196 problemas de olimpíadas de competições anteriores como estatísticas orientadoras, o sistema gerou um repositório de 6,7 bilhões de problemas de geometria , dos quais 4,1 bilhões apresentavam simetria matemática. Três desses problemas foram selecionados para as principais olimpíadas de matemática na China e nos EUA.
Os pesquisadores também testaram as habilidades de resolução do TongGeometry com um conjunto de dados selecionado para o AlphaGeometry (IMO-AG-30) e um novo conjunto de dados (MO-TG-225), ambos servindo como benchmarks. O IMO-AG-30 incluía 30 problemas de 23 anos de competições da IMO, e o MO-TG-225 continha 225 teoremas conhecidos, como o teorema da reta de Euler. O TongGeometry resolveu todos os 30 problemas do benchmark IMO-AG-30, superando a média dos medalhistas de ouro da IMO nesse conjunto de dados específico. Ainda mais impressionante, ele fez isso em 38 minutos, usando recursos computacionais comuns.
"O mecanismo de backend DD do TongGeometry demonstrou uma capacidade de resolução de problemas superior ao DD+AR do AlphaGeometry, atingindo níveis de desempenho próximos aos do AlphaGeometry em geral. Observamos que o sucesso do AlphaGeometry derivou em grande parte de seu mecanismo de backend, com 72,5% das soluções totais alcançadas pelo DD+AR."
"Em contrapartida, o TongGeometry não só resolveu uma proporção maior de problemas (81,3% contra 45,3%), como também utilizou seus modelos neurais de forma mais eficaz para lidar com desafios auxiliares de construção, com apenas 55,2% dos problemas resolvidos somente pelo DD", explicam os autores do estudo.
Potencial educacional e de pesquisa
Embora o TongGeometry não abranja todos os problemas de geometria possíveis, como aqueles que exigem raciocínio algébrico ou combinatório, ele pode ser estendido a outras áreas da matemática. Sua aplicação prática já foi demonstrada em contextos educacionais, nos quais instrutores experientes da IMO revisam e ajustam os problemas, utilizando-os posteriormente com os alunos.
"Essa coleção selecionada é então apresentada aos alunos, servindo a um duplo propósito: fornece uma rica fonte de material de treinamento que ajuda os alunos a dominar tópicos complexos e técnicas específicas de competição, atuando simultaneamente como um poderoso auxílio criativo para os treinadores e ajudando-os a gerar ideias para problemas interessantes e desafiadores para suas equipes", escrevem os autores.
Os autores também destacam o potencial do TongGeometry para ser usado em pesquisas e para o avanço da geometria computacional e do ensino da matemática.
Detalhes da publicação
Chi Zhang et al, Propondo e resolvendo geometria olímpica com busca guiada em árvore, Nature Machine Intelligence (2026). DOI: 10.1038/s42256-025-01164-x
Informações sobre o periódico: Nature Machine Intelligence


.jpg)

